Logikai algebra. 2. rész. Alapvető törvények és funkciók

A logikai algebráról, egyezményekről, szabályokról, műveletekről szóló történet folytatása. Áttérés az érintkező áramkörök alapjaira.

az első cikk George Bullot a logika algebrai alkotójának írták le. A második cikk a logikai algebra alapvető műveleteit és a logikai kifejezések egyszerűsítésének módszereit írja le. A logikai algebra tehát állításokat használ érvekként, és nem azok jelentését, hanem az állítás igazságát vagy hamisságát használja.

A kifejezések írására szolgáló űrlap a logikai algebrában.

Ha az állítás igaz, akkor így írja: A = 1, ha hamis, akkor A = 0 (elvégre nem igaz, hogy a burgonya gyümölcs). Bármely állítás esetén A vagy igaz (A = 1), vagy hamis (A = 0). Itt nem lehet közep. Erről már beszéltünk.

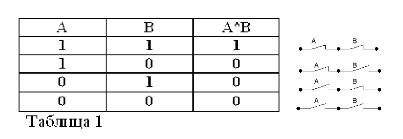
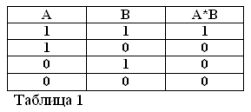
Ha összekapcsol két egyszerű állítást az unióval, és egy összetett kijelentést kap, amelyet logikai terméknek hívnak. Vegyünk két egyszerű mondást: „Három több, mint kettő”, majd „A” betűvel jelöljük, „Három kevesebb, mint öt” - B betűt.

Ezért a „Három több, mint kettő és kevesebb, mint öt” összetett állítás logikus (ebben az esetben a nagybetűs And azt mondja, hogy ez „ÉS” logikai művelet, valamint később a „VAGY” és a „NEM” szövegben). és B. A következő jelöléssel rendelkezik: A ^ B vagy A * B.

Logikai szorzás ("ÉS" művelet).

Elemi algebrai A * A = A2. De Buhl algebrájában A * A = A2 = A, A * A = A, mivel a (*) szorzójel most azt jelenti ... És ... And és And értelmében ... És. Minden tapasztalatunk megerősíti, hogy az A&A ugyanaz, mint egyedül A., ezzel nem lehet egyetérteni. Az állítás igazsága nem változik, ha azt a tényező többször megismétli.

Két állítás szorzata akkor igaz (1-gyel egyenlő), és csak akkor, ha mindkét tényező igaz, és hamis (0-val egyenlő), ha legalább egy tényező hamis. Egyetértenek abban, hogy ezek a szabályok nem ellentmondnak a józan észnek, és emellett teljes mértékben megfelelnek az elemi algebrai szabályoknak:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

Az első egyenlőség a következőképpen szól: ha mind A, mind B igaz, akkor az A * B szorzat igaz. Buhl algebrájában a szorzójel (*) az I. uniót váltja fel.

A logikai termékek nem tartalmazhatnak két, hanem nagyobb számú állítást - tényezőt. És ebben az esetben a termék csak akkor igaz, ha ugyanakkor az összes állítás-tényező igaz.

Logikai hozzáadás (VAGY művelet)

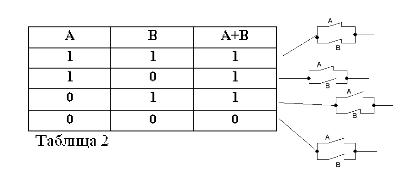
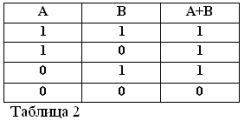
Ha két állítást egy unió köti össze, VAGY. azt az összetett mondatot logikus összegnek nevezzük.

Vegyünk egy példát egy logikai összegre. Mondván: "Ma megyek moziba."

B nyilatkozat: „Ma megyek a diszkóra.” Mindkét állítást hozzáadjuk, és így kapjuk: "Ma megyek a filmekbe, vagy egy diszkóba."

Ezt az összetett állítást a következőképpen jelöljük: A + B = C vagy (A V B) = C.

C-vel egy logikai összeg összetett kijelentését jelöltük.

A vizsgált példában az unió VAGY nem használható kizárólagos értelemben. Valójában ugyanazon a napon eljuthat a moziban és a diszkóba. És itt van a mondás:

„A kertészeti társaság elnöke Petrov vagy Ivanov lesz.” Ez nem logikus összeg, mivel csak az egyik lesz az elnök, a másik pedig a amatőr közönséges kertész.

A logikai összeg V jelét azért választottuk, mert a „vel” latin szó kezdõbetûje, azaz „vagy”, ellentétben a „aut> latin szóval, amely jelentése„ és ”. Most mindenkinek tisztáznia kell, hogy a logikai terméket miért jelzi ^.

Az elemi algebrában van A + A = 2A szabály. Ez a szabály igaz, függetlenül attól, hogy melyik számot ábrázolja az A. betű. A logikai algebrában az A + A = A. szabály felel meg. Egész élettapasztalataink azt mondják, hogy az A VAGY A vagy mindkettő A mondása csak egy újabb és hosszabb módja annak, hogy csak A-t mondjuk.

Mint minden összetett állítás, a két A és B állítás összege is igaz vagy hamis lehet. Az összeg igaznak tekinthető, azaz egyenlő az egységgel, ha legalább az egyik kifejezés igaz:

A + B = 1, ha VAGY A = 1 VAGY B = 1, amely összhangban van a hagyományos számtani módszerrel:

1+0 = 0+1 = 1.

Ha mindkét összesített állítás igaz, akkor az összeget is igaznak tekintjük, tehát a logikai algebrában a következők állnak: (1) + (1) = 1.

A zárójelek itt vannak beállítva, hogy hangsúlyozzák a kiegészítés feltételt, jelentését, és ne számtani.

A két állítás összegét hamisnak tekintjük, és akkor nullával egyenlő, de csak akkor, ha mindkét kifejezés hamis. Innen:

0 + 0=0.

Tehát a két A + B állítás összegét igaznak kell tekinteni, ha igaz, VAGY A, VAGY B, VAGY mindkét kifejezés együtt. Így az OR szót + jelöli.

Emlékeztetve arra, hogy az A és B állítások csak igazak és hamisak lehetnek, és így az 1. vagy 0. igazságmértékesek, a figyelembe vett ÉS és VAGY műveletek eredményeit az 1. és 2. táblázatban foglalhatjuk össze.

A harmadik művelet, amelyet Buhl algebra széles körben használ, a tagadási művelet - NEM. Emlékeztetnünk kell arra, hogy az elemi algebra az ADD, D kivonás, szorzás, osztás és mások műveleteket használja.

Mindegyik A állításhoz megnevezésük van NEM A, amelyet az / A szimbólummal jelölünk. Ez nem kétséges.

Példákat adunk: „Megyünk az erdőbe” A, „Nem megyünk az erdőbe” / A

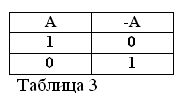
Ha az A állítás igaz, vagyis A = 1, akkor tagadásának / A-nek hamisnak / A = 0. És fordítva, ha valamely állítás hamis, akkor tagadása igaz. Például: „A ló nem eszik széna” / A = 0, „A ló nem eszik széna” (A = 1). Ezt a 3. táblázatban lehet kifejezni.

Meghatározva a tagadás akcióját, és feltételezve, hogy a két A és / A állítás mindig egy igaz, a Boole algebra két új képlete következik:

A + (/ A) = 1 és A * (/ A) = 0.

Vannak más képletek is, amelyek egyszerűsítik az utasítások logikai feldolgozását. Például 1 + A = 1, mivel az összeadás meghatározása szerint abban az esetben, ha egy kifejezés egyenlő az egységgel, akkor az összeg mindig egyenlő. A kapott eredmény nem függ attól, hogy A = 0 vagy A = 1.

A vizsgált három logikai művelet (ÉS, VAGY, NEM) mindegyikének vannak olyan tulajdonságai, amelyek közel állnak az elemi algebra szabályaihoz. Ha mindet megfogalmazunk, akkor 25 szabályt kapunk a logikai algebráról. Ezek elegendőek szinte bármilyen logikai probléma megoldásához. E szabályok nélkül meglehetősen bonyolult a logikai problémák megoldása. A helyes válasz megtalálása a szabályok használata nélkül azt jelenti, hogy találékonysággal és általános érveléssel helyettesítik azokat. A szabályok nagyban megkönnyítik ezt a munkát és időt takarítanak meg.

A cikk keretein belül lehetetlen megvizsgálni mind a 25 szabályt, de azok, akik szeretnék, mindig megtalálják azokat a vonatkozó szakirodalomban.

Mint az 1938-as első cikkben már említésre került, a fiatal amerikai tudós, Claude Shannon „A relé és a kapcsoló áramkörök szimbolikus elemzése” című cikkében először a Boole algebrát használja a relétechnika problémáira. Shannon felfedezése az volt, hogy rájött, hogy a továbbítógépek és az elektronikus számítógépek tervezési módja valójában a matematikai logika egyik ága.

Gyakran előfordul. A tudós évek óta foglalkozik egy olyan problémával, amely teljesen feleslegesnek tűnik honfitársai számára - csak szórakozás. De évtizedek és néha évszázadok telik el, és egy olyan elmélet, amelyre senkinek sem szükséges, nemcsak megszerezi a létezés jogát, hanem anélkül a további fejlődés elképzelhetetlenné válik.

Mi segített Shannonnak másodszor „felfedezni” a logikai algebrát? Az eset? Semmi ilyen.

A hagyományos kapcsolókra és relékre épített relé gépek szeretetének köszönhetően a fiatal tudós összekapcsolta az elfelejtett elméletet az automatikus telefonközpontok feladataival, amelyeken akkor is dolgozott. Később Shannon ugyanazt az „igen vagy nem” elképzelést vezette be a diszkrét üzenetekbe, és megteremtette az alapot a kibernetika egész szakaszának - az információelméletnek.

Buhl algebra nagyon alkalmas volt a reléáramkörök elemzésére és szintézisére. Elég volt elfogadni valódi állításként: „Jel van az áramkörben”, és hamisnak - „Nincs jel az áramkörben”, mivel megjelenik egy új algebra - a jel algebra, a relé áramkör algebra.

Az új algebra csak a relé és a kapcsolási áramkörök figyelembevételére érvényes. Végül is csak az ilyen sémákban teljesül a „van jel” és a „nincs jel” feltétel. Ahol a jel folyamatosan változik, és tetszőlegesen nagy számú közbenső feltételt szerez (ilyen jelet analógnak hívnak), a relé algebra nem alkalmazható. Ezt mindig emlékezni kell. De az elektronikus számítógépek és a kibernetikus gépek többsége a jelfeldolgozás diszkrét elvét alkalmazza, amely az „igen - nem” elemekre épül.

Shannon a „Kapcsolat lezárva” kifejezést igaznak ismerte (1), a „Kapcsolat nyitva” hamisnak (0). Az "algebra" többi részét, beleértve az ÉS, VAGY NEM műveleteket és a 25 szabályt, Shannon kölcsönvette a Boole-tól.

A reléáramköri algebra egyszerűbbnek bizonyult, mint a logikai algebra, mivel csak az "igen - nem" típusú elemekkel foglalkozik. Ezen felül az új algebra vizuálisabb.

Az algebra elemei az érintkezők, amelyeket A, B, C betűkkel jelölünk. Az érintkező zárt - A, az érintkező nyitva - / A (betű vonallal).

A jelölés, amint látja, teljesen a logikai algebrából származik. A nyitott érintkező egy zárt érintkező tagadása. Ugyanaz az érintkező nem lehet zárva és nyitva sem.

Egyetértünk abban, hogy ha bármelyik áramkörben két érintkezőt azonos betű jelöl, akkor ez azt jelenti, hogy mindig ugyanazokat az értékeket veszik fel.

Bármelyik pillanatban vagy egyszerre nyitva vannak, vagy mindkettő zárva van. A legegyszerűbb módja annak, hogy mechanikusan összekapcsolják őket úgy, hogy mindkettő egyszerre nyitva vagy zárva legyen.

Ha az egyik láncban az érintkezés egy másik kapcsolat tagadása, akkor jelentése mindig ellentétes. Például a C és C érintkezők soha nem lehetnek egyszerre nyitva vagy zárva. És az ábrán mechanikusan összekapcsolhatók: ha egyikük kinyílik, akkor a másik bezáródik.

A reléalgebrai megismerést azzal kezdjük, hogy elemezzük az AND, OR és NOT műveleteknek megfelelő legegyszerűbb áramköröket.

Két érintkező (AND működés) szorzata a soros összeköttetés eredményeként létrejövő áramkör: csak akkor záródik be (egyenlő 1-gyel), ha mindkét érintkező zárva van (egyenlő 1-gyel).

A két érintkező (VAGY működés) összege az az áramkör, amely párhuzamos csatlakoztatáskor jön létre: zárt (1-gyel egyenlő), ha az áramkört alkotó érintkezők legalább egyike zárva van (egyenlő 1-gyel).

Ennek az érintkezőnek az ellenkezője (NEM működik) egy 0-os (nyitott) érintkező, ha ez az érintkező 1 (zárt), és fordítva.

Mint a logikai algebrában, ha az érintkezőket A és B betűk jelölik, akkor a két érintkező szorzatát A * B-vel jelöljük, az összeg A + B-vel, az A-vel szemben lévő érintkező pedig / A-val. A fentiek az 1., 2. és 3. ábrán találhatók.

Az AND, OR, and NOT műveleteknek megfelelő táblák érvényessége. most senkinek nem szabad kételkednie.

Nézzünk két példára: 1 * 0 = 0 és 1 + 0 = 1.

Az ábrán látható, hogy egy állandóan nyitott érintkezővel sorosan összekapcsolt állandóan zárt kontaktus egyenértékű egy állandóan nyitott érintkezővel (1 * 0 = 0).

Miután megismerte az érintkező áramkörök aritmetikáját, leírhatja az összes reléáramkört egy képlettel az elfogadott konvenciók szerint. A kibernetikában az ilyen képleteket strukturálisnak nevezik.

Ha bármelyik reléáram szerkezeti képlete 1, akkor egy jel áthaladhat rajta - az áramkör zárva van. Ezzel szemben, ha az áramkör szerkezeti képlete 0, akkor a jel nem megy át rajta - az áramkör megszakadt.Következtetés: Két reléáramkör egyenértékű egymással, ha szerkezeti képletük egyenlő.

A cikk folytatása során megvizsgáljuk az érintkezőáramkörök, a tipikus érintkezőáramkörök és ezek ekvivalenseinek példáit, valamint rajzokat készítünk szerkezeti képletek szerint. Figyelembe vesszük azokat a fő logikai köröket is, amelyek a logikai algebra funkcióit hajtják végre.

A cikk folytatása: Logikai algebra. 3. rész. Kapcsolattartási rendszerek

Boris Aladyshkin

Comments

[#1 Alex]

Köszönöm

Csak egy pont, bekezdés:

"Mint a logikai algebrában, ha az érintkezőket A és B betűk jelölik, akkor a két érintkező szorzatát A * B-vel jelöljük, az összeg A + B-vel, az A-vel szemben lévő érintkező pedig / A-val. A fentiek az 1., 2. és 3. ábrán találhatók."

Hol van a 3. ábra?