kategória: Kiemelt cikkek » Kezdő villanyszerelők
Megtekintések száma: 4409
Megjegyzések a cikkhez: 0
Hogyan számolhatjuk az izzólámpa izzólámpáját névleges üzemmódban?
Mint tudod, a fém hőmérsékletének emelkedésével növekszik annak elektromos ellenállása. Különböző fémek esetében ennek a jelenségnek a kapcsán saját α ellenállás-együtthatója jellemző, amely könnyen megtalálható a referenciakönyvben.
Ennek a jelenségnek az az oka, hogy a fémkristályrács-ionok termikus rezgései fokozódnak a hőmérséklet növekedésével, és az áramot alkotó vezető elektronok gyakrabban ütköznek velük, és több energiát költenek ezekre az ütközésekre. És mivel maga az áram (a Joule-Lenz törvény szerint) a vezető hevítéséhez vezet, akkor mihelyt az áram átvezet a vezetéken, ennek a vezetőnek az ellenállása azonnal növekedni kezd.
Hasonlóképpen, a lámpa izzószálának ellenállása növekszik, amikor azt egy áramforráshoz csatlakoztatják. Nézzük meg a lámpa izzószálának hőmérsékletét a névleges üzemmódban.

A volfrám (ahonnan az izzólámpa izzólámpája készül) hőmérsékleti ellenállási együtthatója α = 0,0045 / K, és az ellenállás változásával (a hőmérsékleti változással együtt) a következő összefüggéssel van társítva:
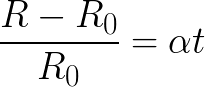
itt van:
Az izzószál R0-ellenállása 0 ° C-on;
Az izzószál R ellenállása a jelenlegi t hőmérsékleten.
Az izzólámpa R0 ellenállása 0 ° C-on még nem ismert, most közvetett módon kell meghatározni. Ehhez először multiméterrel megmérjük a lámpa ellenállását szobahőmérsékleten.
Ezután vessünk egy pillantást a szobahőmérőre, és így megtudhatjuk a szoba levegő hőmérsékletét.
Ha feltételezzük, hogy a lámpa hideg izzószálának pontosan megegyezik a szoba levegőjének hőmérséklete, akkor a lámpa ellenállását 0 ° C-on könnyen meghatározzuk a következő képlet segítségével:
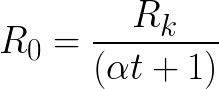
Itt helyettesíteni kell:
t-hőmérséklet a helyiségben (hőmérővel);
A lámpa izzószálának Rk-ellenállása a helyiség aktuális hőmérsékleten (multiméterrel mérhető).
Tehát most ismerjük a lámpa izzóspirálának R0 ellenállását 0 ° C-on. Most, a lámpa névleges teljesítményének és névleges feszültségének ismeretében, tisztán matematikai módon meghatározzuk az Rn névleges ellenállását az alábbi jól ismert képlet szerint:
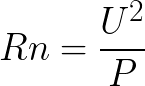
Itt helyettesítjük a közvetlenül a lámpán feltüntetett adatokat:
A lámpa U névleges feszültsége;
P-névleges lámpateljesítmény.
Most az első képletet a következő formába állítjuk, és helyettesítjük az éppen talált Rn névleges ellenállást és az R0 ellenállást 0 ° C-on, valamint a wolframra vonatkozó α = 0,0045 / K hőmérsékleti ellenállási együtthatót (a referenciakönyvből):
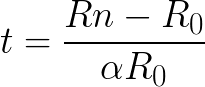
Így megállapítottuk a lámpa izzóspirálának tényleges hőmérsékletét működési állapotban, nem közvetlenül mérve, hanem csak a P névleges teljesítményt, az U hálózat névleges feszültségét, az Rk hidegállóságot, a szobahőmérsékletet és a wolfram-ellenállás hőmérsékleti együtthatóját α.
Lásd még az electro-hu.tomathouse.com oldalon
:
