kategória: Kiemelt cikkek » Érdekes elektromos hírek
Megtekintések száma: 18255
Megjegyzések a cikkhez: 1
A gravitációs energia felhasználása - hogyan lehetséges
A 2000-es évek elején, Lawrence Tseng és Li Cheng, a kínai feltalálók (Lawrence TSEUNG, Cheung LEE) egy módosított ingaelmélet alapján javaslatot tettek az energia gravitációból történő kinyerésére. Rájöttek, hogy ha megnyomja az ingot, akkor azonnal elkezdi vonni a gravitációs energiát.

Ha az F erő lendületét továbbra is rezonanciában alkalmazzák az ingara, akkor az folytatja a gravitációs energia kinyerését. Ez az energia kinyerhető például akkor, ha a fém inga kénytelen áthaladni a mágneses mező vonalain, akkor a mechanikus energia átalakul elektromos energiává. Bár az inga lengő mozgása lelassul, az inga az F erő impulzusának köszönhetően újra felgyorsítható.
Ezen elv hatékonyabb megvalósítása érdekében a lengő mozgás forgással is helyettesíthető. Az ilyen eszközök bárhol működhetnek, még a Holdon is, mivel a gravitációs energia korlátlan.

Az emberek évszázadok óta játszanak hintákkal, de nem is gondolják azt, hogy amikor a hintákat tolják, egyszerre kapják meg a gravitációs energiát. A gyerekek szeretik néhányszor megnyomni a lengőt, majd élesen fékezni őket. Ugyanakkor természetesen észreveszik, hogy a leütési erő sokkal nagyobb, mint amit sokkokkal jelentettek.
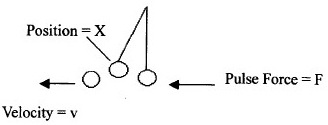
A tankönyvekben ezzel a jelenséggel kapcsolatban nem veszik figyelembe a „gravitációs energia” kifejezést, az erőt csak a rezonanciának tulajdonítják. Feltételezzük, hogy az összes energia az ütésekből az ingahoz jut.
Ez a félreértés évek óta megakadályozta a mérnököket és a tudósokat olyan módszerek és eszközök kifejlesztésén, amelyek évszázadok óta kapnak energiát a gravitációból. Az ilyen találmányoknak nem volt elméleti alapja. Számos ilyen találmányt a szabadalmi hivatalok és a tudósok szerte a világon örökmozgásgépeknek minősítettek, és hagyományosan elutasították.
Eközben a feltalálók a ringató mozgással vagy az ingaval kapcsolatos alapképletek helyes megértésének és a helyes következtetésnek a technikai áttörést fontolóra veszik: az ingot nyomja meg a rezonancia szerint, és a lengő inga hozza ki a gravitációs erőt. Néhány ringatójáték integrált áramköröket használ impulzusok biztosítására.
A lengő játék akkumulátorral vagy fotocellával működik. Ha az inga vagy játék szuszpenzióját rézvezető cseréje helyettesíti, és ezt a vezetőt két mágnes közé helyezik, akkor a rézhuzal áthalad a mágneses mező vonalain és áramot termel. A ringató mozgás lelassul, és a kinetikus energiát elektromos energiává alakítja, de a következő impulzus megint felgyorsítja a terhelést, és kapsz egy egyszerű generátort, amely az energiát kivonja a gravitációból.
A matematika egyszerű. Ha egy kötélen egy m tömegű gömböt veszünk figyelembe, amelyre röviden az F erőt alkalmazzuk, akkor d elmozdulás lép fel. A fizikai törvények az a gyorsítást igénylik, majd F = ma. Az ingara átvitt energia megegyezik az Fd elmozdulás erõsségével. A végső v sebességet Fd = mv2 / 2 értékből kell kiszámítani. Felfüggesztés, súrlódás, gravitáció és légállóság hiányában a golyó egyszerűen v sebességet szerezne, és továbbra is egyenes vonalban haladna. De a gravitáció és a kötél jelenléte miatt a golyó X helyzetbe kerül.
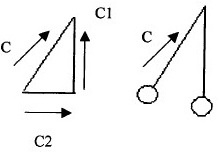
A fenti ábra egy helyzetet ábrázol, amely a körkörös mozgás fogalmát használja. A labda felfelé és balra mozog a C centripetális erő hatására. A C erő két összetevőből áll: a C1 komponens függőleges irányban van. A gravitáció ellen hat, mivel emeli a labdát.
A munka befejeződött, az energia elfogyott, a C2 komponenst vízszintesen, a labda mozgásával ellentétes irányba kell irányítani - a labdára hat, és lelassítja, amíg sebessége nullára nem válik. Munka elvégzett, energia felhasználva.
A C1 alkotóelem úgy tekinthető, hogy hozzájárul a felfüggesztés által elvégzett munkához, amellyel emeli a labdát a gravitáció ellen. Más szavakkal: ez az energia a gravitáció nyilvánvaló energiája. Amint benyomjuk az ingot, a munkát egy gravitáció elleni felfüggesztés hajtja végre. Ezt az energiát meg kell őrizni.
Itt két energiakomponens hatékonyan hat a rendszerre. Az egyik az impulzus energia, amelyet a mozgás elindításához vagy fenntartásához szállítanak. A másik a felfüggesztés által szolgáltatott energia, amely a golyót a gravitáció ellen emeli. Ez azt jelenti, hogy az inga benyomásakor „bevisszük” a gravitációs energiát a rendszerbe. A megfelelő veszteség nélküli inga energiaarányának a következőnek kell lennie:
-
Bejövő energia = Kimenő energia
-
Energiafelhasználás = Energia a lendületről + Energia a gravitációból
-
Kimenő energia = Potenciális energia mgh + Kinetikus energia (mv2 / 2)
Korábban a tudósok nem vették figyelembe ezt az energiát a gravitáció alapján, úgy gondolták, hogy minden energia csak lendületből származik. Így nem engedték meg a mérnököknek, hogy olyan rendszereket fejlesszenek ki, amelyek segítségével közvetlenül kivonják az energiát a gravitációból.
A fenti egyszerű elméleti beállítás sok olyan eszköz megjelenéséhez vezet, amely közvetlenül kivonja az energiát a gravitációból. A szabadalomban a szerzők három példakénti kiviteli példát mutatnak be, azonban tucatnyi út lehetséges.

Az inga
Az inga rézhuzalon van felfüggesztve. Helyezze az ingot a két mágnes közé, és lengő mozgással hagyja áthaladni a mágneses mezőn. Használja a generált villamos energiát a vízszintes sorozatfelvétel elvégzéséhez.
Ez a legegyszerűbb és legnyilvánvalóbb megoldás. A generált elektromos áram azonban nullától a maximálisig változik, és megváltoztatja az irányt. A praktikusabb áramfejlesztő biztosítása érdekében a vezérlést az integrált áramkör igénybevételével kell bonyolítani. Ha a cél csak az elv bemutatása, például egy izzó fényének formájában, akkor ez elég.
kerék
Az elméletben az inga körben forgatható anélkül, hogy megsértené az elméletet. A gyakorlatban az inga helyébe a kerék alakjában levő fém rudak lépnek. Az áramtermelés természetesen lelassítja a forgó kerék mozgását, de egy impulzusos áramkör eltávolítja a többlet energiát a gravitációból, hogy felgyorsítsa a kerék mozgását.
Megfelelő sebességszabályozással a forgás állandó lehet, és az elektromos áram generálása stabil és egyirányú. Hatékony DC generátor lesz. A siker titka a különféle mágnesek és impulzus áramkörök pozicionálásában és vezérlésében rejlik.
A fordulatonkénti gravitációból nyert energia eléri a 2mgR-t, ahol R a kerék sugara. A vett energia ez az értéke kisebb lehet, ha néhány impulzust függőlegesen alkalmaznak. De mindaddig, amíg a gravitációs energia belép a rendszerbe, gravitációtól mentes energiát nyernek.
Kettős kerék és víz
Használhat vizet egy függőlegesen forgó duplakeréken is az energia kiemelésére a gravitációból. Ha nem lenne gravitáció, akkor a víz egyenletesen oszlik meg a kerék külső része mentén. De a gravitáció miatt a víz eloszlása heterogén lesz.
Szélesebb út a mozgás növekvő oldalán és keskenyebb a lefelé mozgó oldalon (ennek oka az a tény, hogy a víz a gravitáció miatt lassabban mozog fel). Használhatjuk a központi tengelyt bordákkal, hogy kivonjuk az energiát az egyszerűen mozgó vízből, vagy ugyanazt a központi tengelyt használhatjuk bordákkal az energia kinyerésére a lefelé forduló vízből.
Ha ismét megnézzük a C centripetalális erő bomlását két C1 és C2 komponensre, akkor C1 emeli a labdát a gravitáció ellen és elvégzi a munkát - a kapott energia átkerül az ingarendszerbe, ez a gravitációból származó energia. A C2 az F erő lendületével szemben irányul, és a golyó v sebességről nullára történő lassítására szolgál. Az erők paralelogramma szerint a C1 sokkal nagyobb lehet, mint C2. Ez azt jelenti, hogy ha több energiát akarunk szerezni a gravitációból, akkor kis, de gyakori F erő impulzusokat kell alkalmaznunk.
A kerék a legjobb megoldás
A legjobb, ha állandó sebességgel forog a kerék. A forgás mechanikus energiáját közvetlenül átalakítják elektromos energiává. A forgási sebesség csökkenni fog, de az impulzusos áramkör több gravitációs energiát „ad ki” a sebesség visszaállításához. Ha több villamos áram szükséges, akkor meg kell növelni a forgási sebességet, és növelni kell az impulzusok számát fordulatonként.
Valami már megtörtént, de nem alaposan
Sok tudós dolgozik az energia területén. Egyesek gravitációs energiát is használnak. Az egyik lehetőség a közismert 02113293.3 számú kínai szabadalom, amelyet 2003. augusztus 13-án adtak ki. Ez a szabadalom a jármű egyenetlen felületen történő mozgatásából származó rezgési energiát használja fel villamosenergia előállítására. Kiegészítheti vagy helyreállíthatja az elektromos autók által fogyasztott energia egy részét, de nem lehet a fő forrása.
Az új elmélet alkalmazható mind rezgő rezonancia rendszerekre, mind rezgő rezonáns rendszerekre. A találmány kitűnő, mivel az elektromos autó fő energiaforrássá válhat.

Egy másik jól ismert kínai szabadalom a 01123526.8, amelyet 2003. március 5-én adtak ki. Ez a szabadalom a henger forgását használja a gravitációs energia kinyerésére az autó központi hajtótengelyéből. Ez egy nagyon hatékony működési módot ír le. A feltaláló azonban nem érti teljesen az elméletet.
Marketing szakirodalmában a kínai filozófia, a nyugati tudomány és a titokzatos kozmikus erők keverékével magyarázta a jelenség megértését. Nem értette, hogy az elmélet egyszerűen a gravitáció „levezetésében” van egy lengő ingból. Lawrence Tseng és Li Cheng által javasolt magyarázat helyesbítette az inga elméletét, és a titokzatos energiaforrásokat hatékonyan kiküszöbölték.
Hasonló elmélet magyarázható az energia kinyerésére a mágneses terekből stb.
A www.rexresearch.com anyagai alapján
© Fordítás angol nyelvről - electro-hu.tomathouse.com
Lásd még az electro-hu.tomathouse.com oldalon
:
